How Hodgkin and Huxley Powered Modern Neuroscience

By Mirella Melo

Abstract

Alan Hodgkin and Andrew Huxley introduced the groundbreaking Hodgkin-Huxley model in 1952, a foundation in neurophysiology. Developed primarily through the voltage-clamp technique and the Nernst equation, the model allows for detailed analysis of nerve action potentials. With technological advances such as the memristor, the model has undergone significant refinements. The memristor's ability to adjust resistance based on past electrical activity has initiated discussions on better representing ion channel properties in biological membranes, merging classical neurophysiology with modern technology. The model's evolution is pivotal in advancing biological understanding and computational modeling.

1. Introduction

Starting in 1939 and resuming from 1946 to 1952 after World War II interruptions, the historic collaboration between Alan Hodgkin and Andrew Huxley revolutionized the field of electrophysiology. Their groundbreaking experiments on the squid giant axon led to the development of the first quantitative model of the nerve action potential, known as the Hodgkin-Huxley model, that earned them the Nobel Prize in Physiology or Medicine in 1963 [1]. Central to their research were the voltage-clamp technique [2], developed by Kenneth Cole and George Marmont in the late 1940s, and the Nernst equation, formulated by Walther Nernst in 1888 as part of his work in physical chemistry [3].

Although the Hodgkin-Huxley model is foundational in neuroscientific research, it has not remained static, undergoing continual refinement in the wake of advancing biological and technological insights. One example of such progress is the integration of memristor theory after its practical realization in 2008 [4]. The memristor, a theoretical concept introduced by Leon Chua in 1971 [5], exhibits variable resistance based on past activity, making it a promising component to represent biological ion channels. This is because ion channels modulate their conductivity in response to the intensity and history of ionic flows [4]. In light of these pivotal advances, from the meticulous work with the voltage-clamp technique to the cutting-edge implications of memristor theory, the enduring legacy of Hodgkin and Huxley's model is beyond question.

2. Results and Discussion

The mid-20th century presented a pivotal advancement in our understanding of neurophysiology. Central to this progress was the work of Hodgkin and Huxley. Building upon the voltage-clamp technique developed by Kenneth Cole and George Marmont [2], they designed experiments on the squid giant axon chosen for its large diameter. The experimental setup is illustrated in Figure 1. It allows for control of the voltage across the axon's membrane while measuring the currents that flow in response to changes in voltage. 

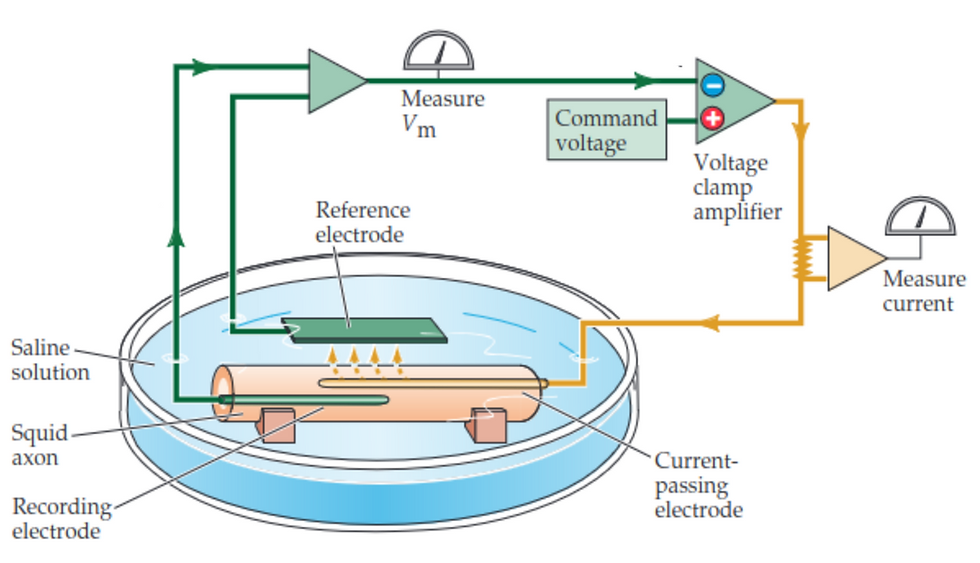
Figure 1: Experimental setup used by Alan Hodgkin and Andrew Huxley, featuring the voltage-clamp technique applied to a squid giant axon [6].

In the experiment, an electrode is inserted into the squid axon to measure the membrane potential Vm. The voltage clamp amplifier receives the Vm signal and compares it with a desired level of potential, known as the command voltage. When the actual membrane potential (Vm​) differs from the command voltage, the amplifier reacts by sending current through another electrode (the current-passing electrode) into the axon. The clamp amplifier continues to adjust the current injection to counteract any difference between the actual and command voltages, maintaining the membrane potential at the set level. As the voltage clamp maintains the desired membrane potential, any ionic currents flowing through the axon's membrane will result in a flow of charge that the system must compensate for by injecting or removing electrons. This compensatory current is measured and is directly proportional to the ionic currents flowing through the membrane channels. By altering the ionic composition of the fluid surrounding the axon and observing the resultant changes in membrane potential, Hodgkin and Huxley could measure the currents caused by sodium and potassium ions separately [1][6].

Beyond the voltage-clamp technique, the Nernst equation (1) was a fundamental part of Hodgkin and Huxley's research [3]. The Nernst equation was proposed by Walther Nernst in 1888 to calculate the electric potential that develops across an ion-permeable membrane due to the concentration gradient of the ion. The ratio RT/zF in the equation, where R is the universal gas constant, T is the absolute temperature in Kelvin, z represents the valence or charge number of the ion, and F is Faraday's constant (the charge per mole of electrons), adjusts the potential to account for these variables, integrating both temperature and ion-specific properties. The natural logarithm of the ratio of external to internal concentrations quantifies (a) the direction and (b) the magnitude of the electrochemical driving force. A positive logarithm result implies that the electrochemical force will drive the ions into the cell and vice versa. A larger logarithm implies a more potent force in ions being pushed or pulled across the membrane.

(1)

From the data collected in the experiment shown in Figure 1 and interpreted through Equation (1), Hodgkin and Huxley made several observations about ionic concentrations and membrane potentials in nerve cells. They confirmed existing knowledge that outside the cell (Extracellular) there is a high concentration of sodium ions Na⁺ and a low concentration of potassium ions K⁺. Contrarily, inside the cell (Intracellular) there's a low concentration of sodium ions and a high concentration of potassium ions. Their findings also supported the already known fact that the cell membrane has an electrical potential difference across it, with the inside being more negative than the outside, characterized by a resting membrane potential of Vm = -70 mV. Furthermore, they provided precise quantification of the equilibrium potentials, calculating the equilibrium potential for sodium (ENa⁺) at +45 mV and for potassium (EK⁺) at -85 mV. The equilibrium potential means no net flow of a specific ion into or out of the cell. Figure 2.A brings these values and illustrates the selective íon channels, which are protein structures that allow only specific ions to pass through, and the sodium-potassium pump that actively moves three sodium ions out of the cell and two potassium ions into the cell against their respective concentration gradients. The pump establishes the gradients and the selective ion channels use these gradients to generate and regulate the membrane potential [6][7]. 

Figure 2: Schematic representation of the electrical circuit model for a neuron's membrane as described by the Hodgkin-Huxley model [7].

While Figure 2.A shows the biological model, Figure 2.B presents its equivalent in an electrical circuit, a groundbreaking contribution by Hodgkin and Huxley from the voltage-clamp experiment (see Figure 1) [8]. It describes how changes in membrane potential activate and deactivate ion-specific channels. The neuron's membrane exhibits a property known as membrane capacitance (Cm), equivalent to a capacitor in an electrical circuit, which allows it to store electrical charge. In addition, there is a voltage difference across the cell membrane, the membrane potential (Vm). Each type of ion channel in the membrane can be considered a resistor (RNa, RK, and RL), limiting current íon flow of sodium (INa), potassium (IK), and other ions through leak channels (IL). Furthermore, each type of ion has an associated equilibrium potential (ENa, EK, and EL), also known as the Nernst potential. It is important to highlight that different polarities for ENa, EK, and EL are due to the direction and magnitude of the electrochemical gradients for each ion type [7][8].

Mathematically, Equation 2 reflects this dynamics of electrical behavior across the cell membrane, where CmdV/dt​ represents the capacitive current associated with the charge stored on the membrane and Iion​ accounts for the ionic currents flowing through ion-selective channels. The capacitive current is proportional to the rate of change of the membrane potential Vm over time, illustrating how quickly ions charge or discharge the membrane's capacitance. The ionic current is a steady flow governed by the permeability of the membrane and the driving forces on ions. The total membrane current I is the sum of these two components, encapsulating the electrical state of the neuron as it processes and responds to physiological stimuli [8].

 (2)

Although the Hodgkin-Huxley model has been widely accepted and utilized since its publication, it has undergone various refinements. The concept of the memristor, introduced by Leon Chua in 1971, offered a new perspective on electrical components with memory, which has led to recent discussions about the potential for memristors to represent the properties of ion channels in biological membranes more accurately. These discussions have gained traction following the practical demonstration of a memristor by HP Labs in 2008 [9]. Unlike a resistor whose resistance is a fixed value for a given temperature and material, the memristor exhibits a resistance that can vary according to the amount and direction of electric charge that has previously passed through it. This property allows the memristor to “remember” its past electrical states even when the power is turned off. As ion channels in biological membranes exhibit a dependency on their activation history (for example, their response to past voltage changes), the memristor provides a more accurate electronic analogy. [4][9]

3. Outlook and relevance of work

The Hodgkin-Huxley model [8], developed through meticulous experiments and mathematical rigor, has firmly established itself as a fundamental framework in neurophysiology, setting the stage for insights into cellular mechanisms of nerve function, such as ion channel behavior and action potential propagation. In recent discussions, the memristive Hodgkin-Huxley model [4] has emerged as an innovative fusion of classical neurophysiology and cutting-edge technology. This approach not only reconciles abstract mathematical equations with physical systems but also replicates the electrical characteristics of neuronal behavior, offering a more integrated understanding of nerve function.

Advancements in computational models and neuromorphic computing, which mimic the human brain's architecture and functions [10], have been significantly influenced by the biological principles of the Hodgkin-Huxley model, connecting them directly to the forefront of artificial intelligence technology. As we delve into the potential of memristors, we see a future where the principles of neural conduction inform the design of memory and processing systems, symbolizing a convergence of biological inspiration and technological innovation.

References

[1] Schwiening, Christof J. "A brief historical perspective: Hodgkin and Huxley." The Journal of Physiology 590.Pt 11 (2012): 2571.

[2] Cole, Kenneth Stewart. Dynamic electrical characteristics of the squid axon membrane. Naval Medical Research Institute, National Naval Medical Center, 1950.

[3] Nernst, Walther. "Zur kinetik der in lösung befindlichen körper." Zeitschrift für physikalische Chemie 2.1 (1888): 613-637.

[4] Sah, Maheshwar Pd, Hyongsuk Kim, and Leon O. Chua. "Brains are made of memristors." IEEE circuits and systems magazine 14.1 (2014): 12-36.

[5] Chua, Leon. "Memristor-the missing circuit element." IEEE Transactions on Circuit Theory 18.5 (1971): 507-519.

[6] Purves, Dale, et al. Neuroscience. 6th ed., Sinauer Associates, 2018.

[7] Desbiolles, B. X. E., et al. "Intracellular recording of cardiomyocyte action potentials with nanopatterned volcano-shaped microelectrode arrays." Nano letters 19.9 (2019): 6173-6181.

[8] Hodgkin, Alan L., and Andrew F. Huxley. "A quantitative description of membrane current and its application to conduction and excitation in nerve." The Journal of Physiology 117.4 (1952): 500.

[9] Strukov, Dmitri B., et al. "The missing memristor found." nature 453.7191 (2008): 80-83.

[10] Mead, Carver, and Mohammed Ismail, eds. Analog VLSI implementation of neural systems. Vol. 80. Springer Science & Business Media, 2012.